
Les 6n +- 1 divisent la somme des entiers naturels²
« La somme des entiers naturels mis au carré, n’est divisible, que lorsque le diviseur est un nombre de la forme 6n +- 1« , c’est la découverte de cette propriété des 6n +- 1, qui m’a permis de résoudre, l’un des plus vieux problème des mathématiques.
L’ensemble des 6n +- 1, est l’ensemble des nombres premiers supérieur à 3, ayant tous la particularité d’êtres, des nombres de la forme 6n – ou + 1
A 6n + et – 1, il n’y a que deux sortes de nombres; soit c’est un nombre premier, soit c’est le produit de (6n+-1) x (6n +- 1) = 6n +- 1
l’apparition d’un nouveau nombre premier, est conditionné par l’absence de multiples des nombres premiers précédents.
Exemple simple:
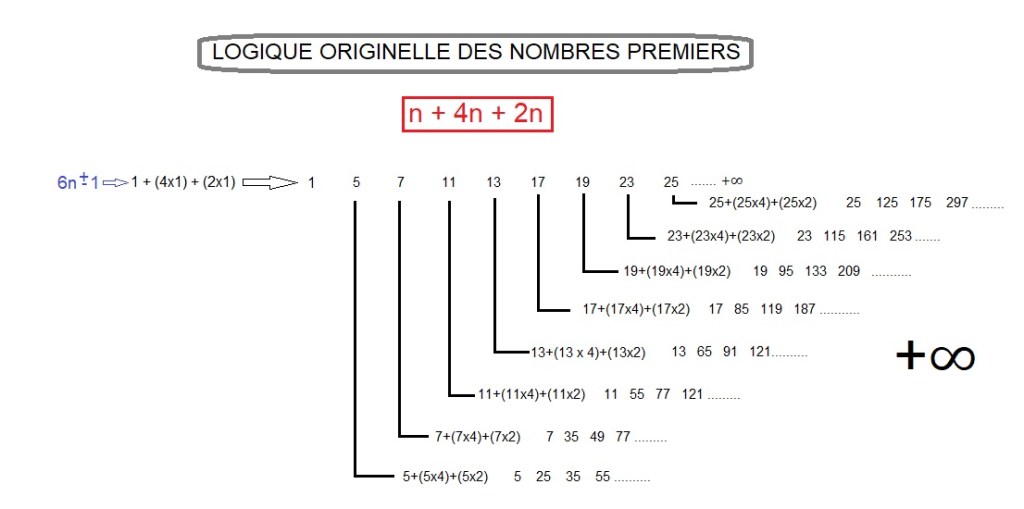
Si nous prenons 5 et 7, qui sont les deux plus petits nombres premiers, de la forme 6n +-1 et que nous faisons les opérations suivantes: 5 x 5 et 5 x 7, qui donnent les résultats 25 et 35, nous pouvons affirmer avec certitude, qu’entre 25 et 35, les nombres de la formes 6n +- 1, seront obligatoirement premiers. Les deux seuls nombres de la forme 6n +- 1, situés entre 25 et 35, sont 29 et 31 et ce sont bien des nombres premiers.
Deuxième exemple toujours avec 5 et 7:
Entre (35)5 x 7 et (49)7 x 7, tout les 6n +- 1 compris dans cet intervalle, sont premiers et ces nombres premiers sont: 37; 41; 47
Au fur et à mesure que l’on va dans les grands nombres, les nombres premiers disparaissent définitivement et seuls restent les composites.
Petit problème à résoudre, prenez votre temps j’y travaille encore:
Si l’on considère la logique des 6n+-1, déterminer à quel moment les composites occuperont 100% des 6n+-1?, Si vous arrivez à répondre à cette question, c’est que vous avez aussi réussi à déterminer la valeur du dernier nombre premier et que vous avez trouvez la formule, qui élimine les composites, pour ne laisser que les premiers .
Les 6n +- 1, non premiers sont les produits de la multiplication de deux 6n +- 1

Théorème de la répartition des nombres premiers.
Énoncés:
Les nombres premiers supérieurs à 3, sont de la forme 6n+1 ou 6n-1
Les 6n+1 ou 6n-1 non premiers, sont le produit de la multiplication de deux 6n+1 ou 6n-1.
Proposition 1:
Soit K un nombre entier positif, si K n’est ni multiple de 2, ni multiple de 3, alors K est de la forme 6n+1 ou 6n-1.
Démonstration:
Par l’absurde:
Supposons que les nombres premiers supérieurs à 3, ne soient pas de la forme 6n+-1, cela signifierais qu’ils sont soit de la forme: 6n; 6n+-2 ou 6n+-3 et donc , qu’ils seraient multiple soit de 2, soit de 3, ce qui est absurde.
Par la logique:
Pour commencer faisons l’observation, que 6 est un multiple commun à 2 et 3, que les nombres de la forme 6n-1, sont exactement identiques aux nombres de la forme 6n+5.
Remarquez aussi que, étant donné un nombre, il n’y a que 6 possibilités :
6n ; 6n+1 ; 6n+2 ; 6n+3 ; 6n+4 et 6n+5.
Les nombres de la forme 6n, 6n+2 et 6n+4, sont multiples de 2 et les nombres de la forme 6n ; 6n+3 sont multiples de 3.
Alors, si K n’est multiple ni de 2,ni de 3, alors K est de la forme 6n+1 ou 6n+5, c’est-à-dire, de la forme 6n+1 ou 6n-1.
Corollaire: Si P est un nombre premier plus grand que 3, alors P est de la forme 6n+1 ou 6n-1.
Proposition 2 : Le produit de deux nombres entiers de la forme 6n+1 ou 6n-1, est un nombre de la forme 6n +1 ou 6n -1
Démonstration
Il y a 8 cas de figures possibles à vérifier:
(6x – 1) (6x – 1) = 6 (6x² – 1 – 1) + 1
(6x -1) (6x + 1) = 6 (6x² – 1 + 1) – 1
(6x + 1) (6x + 1) = 6 (6x² + 1 + 1) + 1
(6x + 1) (6x – 1) = 6 (6x² + 1 – 1) – 1
(6x – 1) (6y – 1) = 6 (6xy – x – y) + 1
(6x – 1) (6y + 1) = 6 (6xy + x – y) -1
(6x + 1) (6y + 1) = 6 (6xy + x + y) + 1
(6x + 1) (6y – 1) = 6 (6xy – x + y) -1
Corollaire: Si P et Q sont deux nombres premiers plus grands que 3, alors PQ sont de la forme (6n) + 1 ou (6n) – 1.
Démonstration
P et Q sont deux nombres premiers plus grand que 3, par le corollaire de la proposition 1, ils sont de la forme 6n+1
ou( 6n ) -1.
Par la proposition 2, PQ et leurs produits sont de la forme (6n) + 1 ou (6n) – 1.
Proposition 3
Soit A, B et K des nombres entiers. Si K est de la forme (6n)+1 ou (6n)-1 et K = AB ; alors A et B sont aussi de la forme (6n)+1 ou (6n)-1.
Démonstration :
Si K est de la forme (6n)+1 ou(6n)-1, alors K n’est multiple ni de 2, ni de 3. Par conséquent , si K = AB, alors A et B ne sont multiples ni de 2, ni de 3.
Par la proposition 1, A et B sont de la forme (6n)+1 ou (6n)-1.
Corollaire : Les nombres entiers positifs plus grand que 1 et de la forme (6n)+1 ou (6n)-1, sont soit des nombres
premiers, soit le produit de deux nombres entiers, eux aussi de la forme (6n)+1 ou (6n)-1. Ce corollaire est une
conséquence immédiate de la définition de nombre premier et de la proposition 3.
Pourquoi les carrés des 6n+-1, sont tous des 6n+1 et qu’il n’y a aucun carré de la forme 6n-1?
Réponse:
Puisque les carrés, sont la somme d’un seul et même nombre, multiplié par lui même et que ce nombre ne changera jamais de signe, soit c’est (+), soit c’est (-), il n’y a que deux solutions possibles:
(6n+1)x(6n+1)=(6n+1) ou (6n-1)x(6n-1)= (6n+1)
