
Ces nombres fascinants, dont personne jusqu’à aujourd’hui, n’a réussi à définir les règles, qui déterminent leur positionnement, par rapport, aux autres entiers naturels.
Depuis le début de l’ère des mathématiques, l’énigme de leurs répartition fascine.
Pourquoi? Ce problème, tarde tant de temps à trouver sa solution, pourquoi personne ne trouve ?
POURQUOI LE MODE DISTRIBUTION DES NOMBRES PREMIERS, EST RESTÉ INTROUVABLE ?
Si personne n’a trouvé, c’est parce-ce, qu’il leurs manquaient l’information essentiel; ils ignoraient l’existence et la logique des 6n +- 1 et ils n’ont tenu compte, que de l’ensemble des nombres premiers en y incluant 2 et 3, or malgré, qu’ils soit premiers, 2 et 3 n’ont aucun rapport avec la distribution des nombres premiers, qui leurs sont supérieurs, pour cause : Ce sont les seuls nombres premiers, qui ne soient de la forme 6n -+ 1.
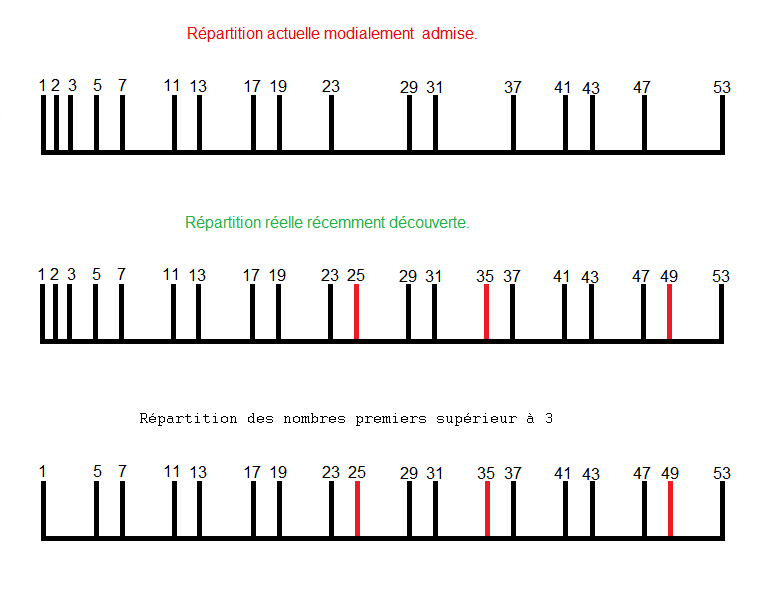
Ératosthène est celui , qui s’est le plus rapproché de la solution avec son crible, mais, il ne l’a pas utilisé de la bonne façon; Il l’a utilisé pour isoler les nombres premiers en faisant un crible complet , alors, qu’il aurait pu l’utiliser, pour déterminer leurs positionnement, dans l’ensemble des entiers naturels. Voyons comment il aurait du procéder.
CRIBLE PARTIEL
Établissons la suite des entiers naturels borné à 100, faisons un crible partiel, éliminons les multiples de 2 et 3 qui sont les plus petits diviseurs en dehors du 1, qui lui divise tout, voilà ce que l’on obtient.
1; 5; 7; 11; 13; 17; 19; 23; 25; 29; 31; 35; 37; 41; 43; 47; 49; 53; 55; 59; 61; 65; 67; 71; 73; 77; 79; 83; 85; 89; 91; 95; 97
Maintenant nous avons deux suite, nous allons prendre les nombres de notre première suite, celle des nombres premiers, puis nous allons les retrancher de la deuxième suite, celle des rescapés du crible de 2 et 3 et nous voilà avec une troisième suite qui correspond à cela:
1; 25; 35; 49; 55; 65; 77; 85; 91; 95
Donc, dans cette dernière suite, nous avons éliminé, tout les nombres premiers inférieurs à 100 et tout les multiples de 2 et 3. Qu’est-ce qu’il nous reste?
Après analyse et réflexion, nous pouvons déduire, que ces nombres correspondent aux produits de la multiplication des rescapés du crible partiel de 2 et 3.
Décomposition de la spirale des entiers naturels
Ci – dessous, j’ai décomposé la spirale des entiers naturels, nous pouvons admirer la beauté des figures, de ses différents constituants.

A quoi correspondent ces nombres ?
Si vous trouvez, laisser un commentaire. Sinon découvrez la réponse ici

Laisser un commentaire