nombrespremier.fr

For over 3000 years, the greatest mathematicians have been looking for a way to explain the distribution of prime numbers, how they work?

Why has no one yet managed to solve this enigma?

What is the element that has misled researchers of the caliber of Euclid, Sophie Germain, Pythagoras, Euler, Gauss, Riemann, Mersenne, Erathostène, Goldbach and many others, the list is not exhaustive.

The element that has misled all these illustrious representatives of the science of mathematics is that they were inspired by previous studies to do their own research, they only took into account the visible elements, known from the sequence of prime numbers, including 1; 2 and 3, but they could not solve this enigma with these elements alone.

They were missing the key piece of the puzzle.

The set of natural numbers is actually composed of three sets, quite distinct from each other, but nevertheless coexisting in symbiosis. So it is a question of determining the logic of the 3 sets, 2 of them are known.

But the 3rd set was unknown until I discovered its existence on October 29, 2012, by doing an operation that apparently had never been done, otherwise the mystery of the distribution of prime numbers would have been solved.

Solving the problem.

Let’s start by bounding the set of natural numbers, to obtain a smaller set, easier to study, than the infinite set.

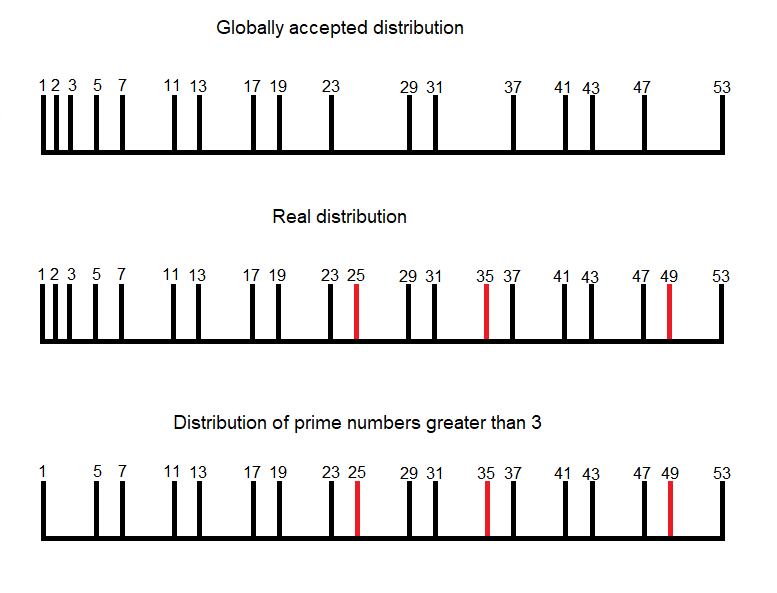
Let’s use part of Eratosthenes’ reasoning, by making a sieve, but just a partial sieve, to determine their positions in the set of natural numbers.

To do this, let’s use the two smallest numbers outside of 1, which are 2 and 3, and let’s sieve our mini set of natural numbers. Once this is done, we will already have a more precise idea of ​​their locations within the set of natural numbers and after analysis, we will be able to deduce the rules that govern their distribution.

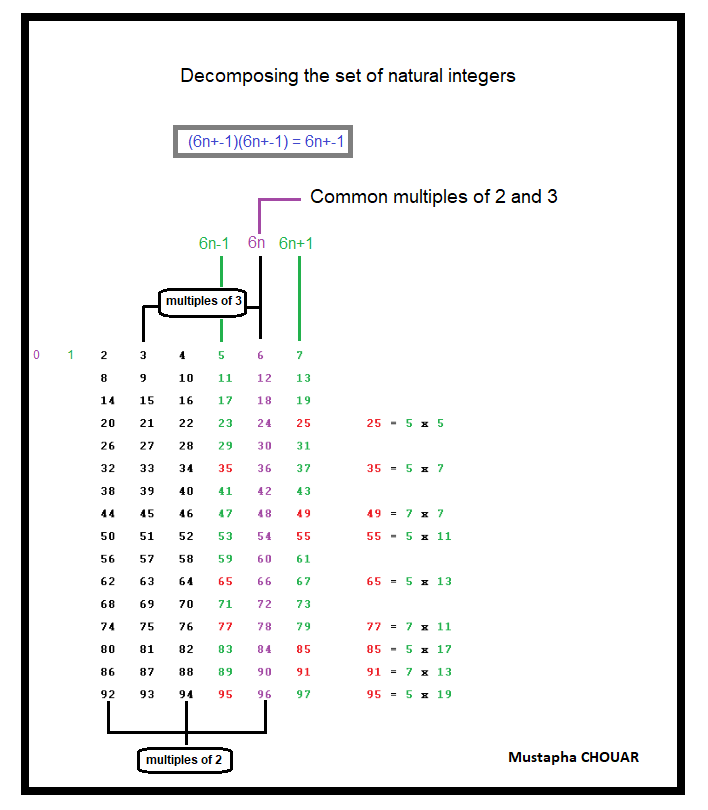
We can see in the illustration below that once the multiples of 2 and 3 are eliminated, there is only one category of numbers left, all of which are of the form 6n +- 1

6n +- 0; 1; 2; 3

6n +- 0: Corresponds to multiples common to 2 and 3

6n +- 1: These are the prime numbers greater than 3 and the multiples they produce when multiplied together.

6n +- 2: These are the multiples of 2

6n +- 3: These are the multiples of odd 3

Mathematical truth:

Numbers of the form 6n +- 1 cannot be divided by 2 and 3, because only a 6n +- 1 can divide another 6n +- 1.

Why 6 and why 1?

6 is the least common multiple of 2 and 3, since 2 x 3 = 6,

Why plus or minus 1 unit, answer:

6 -1 and 6 + 1, gives a result that can’t be divided by 2 or 3, and that’s logical.

For this number to be divisible by 2, we would have had to either add or subtract 2, and to obtain a number divisible by 3, we would have had to either add or subtract 3.

At this point, we can deduce from the above that 2 and 3 are the only prime numbers that are not of the form 6n+-1.

That 3 is the only odd prime not of the form 6n + or – 1.

That 6n + – 1 are infinite, since multiples of 6 are infinite.

That 6n + and – 1 are twins when (n) has the same value.

That there are 4 possible kinds of twins.

That the squares of prime numbers greater than 3 are all of the form (6n +1).

That 2 is the only even prime number.

That the number of prime numbers below a given limit is inversely proportional to the number of non-prime 6n + – 1 remains to be demonstrated, but to my mind it’s logical, since the number of some (primes) depends on the number of others (composites).

It’s the parable of the filling vase! Let’s suppose we have an empty vase, and let’s suppose that this emptiness in the vase is the set of prime numbers. We add water, which represents the 6n+- 1 composites, and the more water we add, the less space is left for the prime numbers.

The set of natural numbers can be summarized as:

6n +- 0; 1; 2; 3

6n +- 0: Corresponds to the multiples common to 2 and 3

6n +- 1: These are the prime numbers greater than 3 and the multiples that they produce when they multiply together.

6n +- 2: These are the multiples of 2

6n +- 3: These are the multiples of 3 odd numbers

Mathematical truth:

Numbers of the form 6n +- 1 cannot be divided by 2 and 3, because only a 6n +- 1, can divide another 6n +- 1

Why 6 and why 1?

6 is the LCM or least common multiple of 2 and 3, since 2 x 3 = 6,

Why plus or minus 1 unit?, answer:

6 -1 and 6 + 1, gives a result, which cannot be divided by 2 or 3 and it is logical.

For this number to be divisible by 2, it would have been necessary to either add or subtract 2 and to obtain a number divisible by 3, it would have been necessary to either add or subtract 3.

At this point, we can deduce from the above, that 2 and 3 are the only prime numbers, which are not of the form 6n+-1.

That 3 is the only odd prime number, which is not of the form 6n + or – 1.

That the 6n + – 1 are in infinite quantity, since the multiples of 6 are infinite.

That the 6n + and – 1 are twins when (n) is of the same value.

That there are 4 possible kinds of twins.

That the squares of the prime numbers greater than 3, are all of the form (6n +1).

That 2 is the only even prime number.

That the number of prime numbers, less than a given limit is inversely proportional, to the number of 6n + – 1 non-primes, this remains to be demonstrated, but it is logical in my opinion, since the number of some (the prime numbers), depends on the number of others (the composites).

It is the parabola of the vase that fills up! Suppose we have an empty vase and suppose that this emptiness, in the vase, is the set of prime numbers, we add water, which represents the composite 6n + – 1, the more water we add, the less room there is for the prime numbers and when the vase is full the water takes the ascendant and overflows the vase.

Goldbach’s conjecture

We can now confirm and demonstrate the Goldbach conjecture, given that the prime numbers greater than 3 are all of the form 6n + – 1.

Goldbach’s conjecture

Now that we know the logic of the 6n + – 1, we are able to confirm and demonstrate this conjuncture.

Let’s not forget that 1 is the first 6n +1, when (n) has the value 0.

(6n +- 1)(6n +- 1) = 6n +- 1

If you liked it, please like and subscribe. Thank you.