Nous savons à présent, qu’a 6n+- 1 il n’y a, que deux sortes de nombres:
Les nombres premiers supérieurs à 3 et le produit de ces mêmes nombres , lorsqu’ils se multiplient entre eux.
Les 6n +- 1, sont les seuls emplacements, laissés vacant par 2 et 3, c’est la seule possibilité, pour les nombres premiers supérieurs à 3, de pouvoir prendre place dans l’ensemble des entiers naturels.
Et c’est logique, puisque 6 est le plus petit multiples communs à 2 et 3, donc 6n -1 et 6n +1, ne seront jamais divisibles ni par 2, ni par 3.
2 divise les 6n; 6n+-2; 6n +-4
Tandis que 3 divise les 6n; 6n +-3.
Donc il ne reste plus que 6n+-1 et 6n+- 5; à remarquer que 6n+5 et 6n-1, sont semblables.
Pour terminer, il faut préciser que, quand un nombre de la forme 6n +- 1, se multiplie avec un autre nombres de la forme 6n +-1, le résultat ne peut pas se positionner a 6n; 6n +- 2 ou 6n+-3, puisque, n’étant pas multiple de 2 ou de 3, les seuls possibilités qui lui reste, c’est 6n+1 et 6n-1 .
Les nouveaux nombres premiers, ne peuvent prendre place, que là ou leurs prédécesseurs, ne positionnent pas un de leurs multiples.
Les 6n+-1 composites, sont calculables de différentes façons, puisque en mathématiques, il y a différentes méthodes pour résoudre un problème et obtenir la même solution.
Pour le moment, toutes les méthodes, que j’ai définis m’ont invariablement mené au même résultat. A savoir, elles me donnent les 6n +- 1, premiers et composites, indistinctement, sans moyens de les différenciés.
Cependant malgré, que je n’ai pas encore trouvé la formule, qui permet d’isoler les 6n +- 1 premiers, je sais comment calculer les 6n +- 1 composites il suffit d’utiliser la formule:
P+(4P) + (2P)
Et nous obtenons ainsi, la raison de la suite des 6n +- 1 composites, d’un 6n +- 1 premier.
Exemple avec le premier 6n – 1 ou (n) a pour valeur: 1
(6 x 1) – 1 = 5
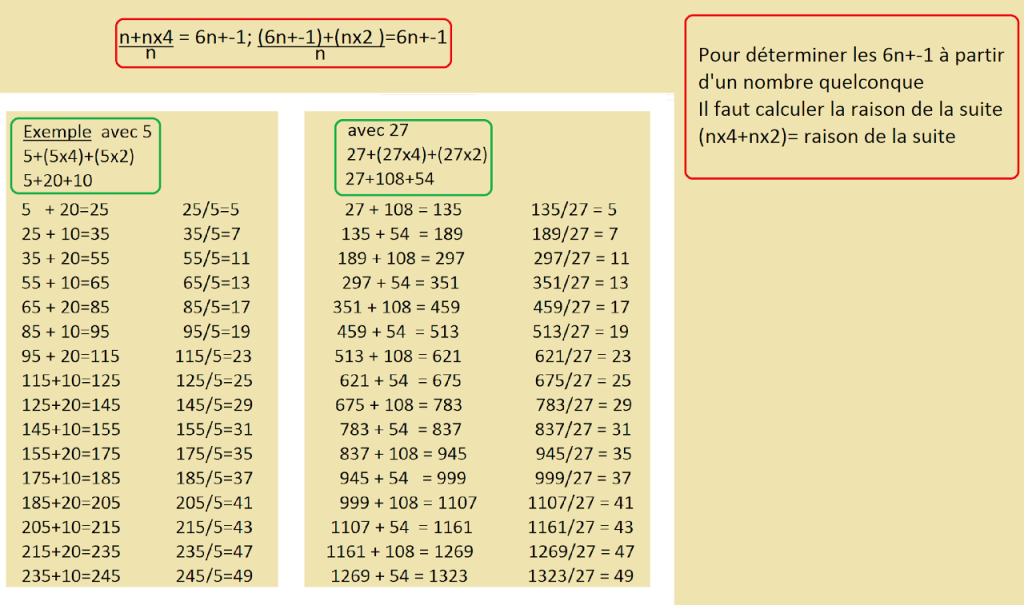
5 + ( 5 x 4) + (5 x 2) ; 20 et 10 sont la raison de la suite des 6n +- 1 composites issue de 5, nous obtenons la suite suivante: 5 + 20 + 10 + 20 +10 + 20 + 10…etc Cela donne:
5; 25; 35; 55; 65; 85; 95; 115; 125 …etc Quand on divise ces résultats par 5, nous reconstituons la suite des 6n +- 1 supérieurs à 1, puisque 1 est le premier 6n +1, lorsque (n) à pour valeur : 0
A savoir.
Les nombres impairs, peuvent se décomposer en 3 catégories de nombres bien distinctes l’une de l’autre.
Il y a les nombres impair multiples de 3
Il y a les 6n +- 1 premiers.
Et pour terminer les 6n +- 1 composites, qui sont les produits de:
(6n +- 1) x (6n +- 1) = (6n +- 1)

A noter : Tout les 6n+- 1, ont leurs carré à 6n + 1. En effet :
(6n-1)x(6n-1)= 6n+1
(6n+1)x(6n+1)=6n+1
Les intervalles séparant les carrés, sont multiples de 24, en commençant par 1+24n
Si différent calculs logiques, mènent au même résultat, c’est que ce résultat est vrai et important, puisque tout mène à lui.
C’est le cas des 6n+-1
Si vous aimez, liker, partager et commenter

Laisser un commentaire